Qwerty Rides Again
The sometimes maligned Qwerty keyboard has found a new calling on mobile devices. While it is easy to argue that other layouts (notably Dvorak) are more effective for typing on a full sized keyboard, those features that make it relatively ill suited for such a task actually improve Qwerty’s usability in a mobile, touchscreen environment; frequently used keys are further apart, so a mistyped word is more easily mapped by corrective software to the right match. The truth is in the numbers, but first a bit of backstory.
Legend has it that the Qwerty keyboard layout was devised, at least in part, to slow typing down. Regardless of the truth of this, Dvorak practitioners firmly believe that their layout provides for faster typing and while this claim has been disputed by some, at the least there seems to be some conflict in the research literature. I put together a program to calculate a measure of the difference in work required to type words on a Qwerty or Dvorak keyboard. Quite simply, I gave a weighting to each key equal to the distance a finger has to move in order to strike it and then ran through the entire Webster’s Dictionary (conveniently located at /usr/share/dict/words on OS X) to calculate the average “work” done per word. The results are quite convincing.
Average Work Per Word
| Qwerty | 7.509 |
|---|---|
| Dvorak | 4.586 |
Breakdown of Work Per Word
| No Move | Move 1 | Move 2 | |
|---|---|---|---|
| Qwerty | 2.467 | 6.727 | 0.391 |
| Dvorak | 5.132 | 4.321 | 0.132 |
This is a resounding win for Dvorak, clearly, one doesn’t have to move one’s fingers as much to type in Dvorak than in Qwerty. But the question then remains: what effect does this information have on the reliability of typing on a small touchscreen keyboard? In this case, not much. The idea with a touchscreen keyboard like the iPhone’s is that to some degree, instead of simply touching a sequence of buttons, you are touching the screen in a pattern. If you are off a bit in the exactness of your taps, the overall pattern is usually distinct enough for the software to determine what you meant. My reasoning is that Qwerty, with its frequently used keys relatively far apart, makes the patterns for individual words more easily recognizable. Since Dvorak puts important keys closer together, it is more likely that words will share a similar pattern.
In order to test this hypothesis, we can compare the distance between letters in words of the same length. For example, the words lone and maid:
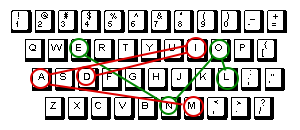
By adding up the distance betweens the M and L, the A and O, the I and N, the D and E, and averaging the values you find the average distance between letters in the two words. (In this case, 2.9749) I wrote up a program to do this for every pair of words in the dictionary and the results confirmed my suspicions. I only ran the script for two, three and four letter words as comparing all possible pairs of words gets to be a pretty heavy computational task after that; O(n²) is a harsh mistress.
Average Distance Between Letters
| 2 Letters | 3 Letters | 4 Letters | |
|---|---|---|---|
| Qwerty Average Distance | 3.3027 | 3.2605 | 3.3035 |
| Dvorak Average Distance | 3.3705 | 3.1924 | 3.2774 |
While the Dvorak average for two letter words is in fact longer than that for Qwerty, for the other lengths, Qwerty has a slight edge. It would be helpful, of course, to see the results for more lengths, I may get around to that in a follow up. I also calculated the number of “almost matches” where an almost match is a pair of words on a particular layout with the distance between each letter pair of one or less. These results are a bit more striking.
Number of Almost Matches
| 2 Letters (9,316 Pairs) | 3 Letters (783,126 Pairs) | 4 Letters (11,982,960 Pairs) | |
|---|---|---|---|
| Qwerty Almost Matches | 665 | 18,068 | 82,212 |
| Dvorak Almost Matches | 766 | 21,400 | 104,459 |
Dvorak, even for two letter words, has more “almost matches” than Qwerty. These results confirm the hypothesis that Qwerty has an edge over Dvorak on small, touchscreen keyboards where the pattern of a word is used to recognize it. There are obviously other important reasons for Qwerty’s current and future dominance of such keyboards not the least of which is its near universal familiarity, but this evidence further justifies it.
For the curious, here are the two programs I used to calculate these numbers: fingers.py & similar.py